B - 2点間距離の最大と最小 ( Maximum and Minimum )
Editorial
 /
/ 
平面上に N+1 個の点があり、それぞれ 0 から N までの番号が付けられています。
それぞれの点の位置はわかりませんが、0 以上 N 未満の整数 i について、i 番の点と i+1 番の点の距離 d_i はわかっています。
0 番の点と N 番の点の距離としてとりうる値の最大と最小を求めてください。
入力は以下の形式で標準入力から与えられる。
出力は標準出力に出力し、2 行からなる。
1 行目には、0 番の点と N 番の点の距離としてとりうる最大値を出力せよ。
2 行目には、0 番の点と N 番の点の距離としてとりうる最小値を出力せよ。
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 10^{-3} 以下であれば許容する。
なお、最後には改行を出力せよ。
 /
/ 
Time Limit: 2 sec / Memory Limit: 64 MB
問題文
それぞれの点の位置はわかりませんが、0 以上 N 未満の整数 i について、i 番の点と i+1 番の点の距離 d_i はわかっています。
0 番の点と N 番の点の距離としてとりうる値の最大と最小を求めてください。
入力
N
d_{0}
d_{1}
:
d_{N-1}
- 入力は N+1 行からなる。
- 1 行目には点の番号の最大を表す整数 N(1≦N≦500) が与えられる。
- 2 行目から N+1行目までの i+2 行目 (0 ≦ i < N)には、i 番と i+1 番の点の距離を表す整数 d_i(1≦d_i≦30,000) が与えられる。
出力
1 行目には、0 番の点と N 番の点の距離としてとりうる最大値を出力せよ。
2 行目には、0 番の点と N 番の点の距離としてとりうる最小値を出力せよ。
誤差は絶対誤差あるいは相対誤差の少なくとも片方が 10^{-3} 以下であれば許容する。
なお、最後には改行を出力せよ。
入力例 1
1 1024
出力例 1
1024 1024
- 入力より 0 番の点と 1 番の点があり、それらの間の距離は 1024 であることが分かります。
- 求める距離は、0 番の点と 1 番の点の間の距離なので最大値も最小値もともに 1024 です。
入力例 2
3 3 4 5
出力例 2
12 0
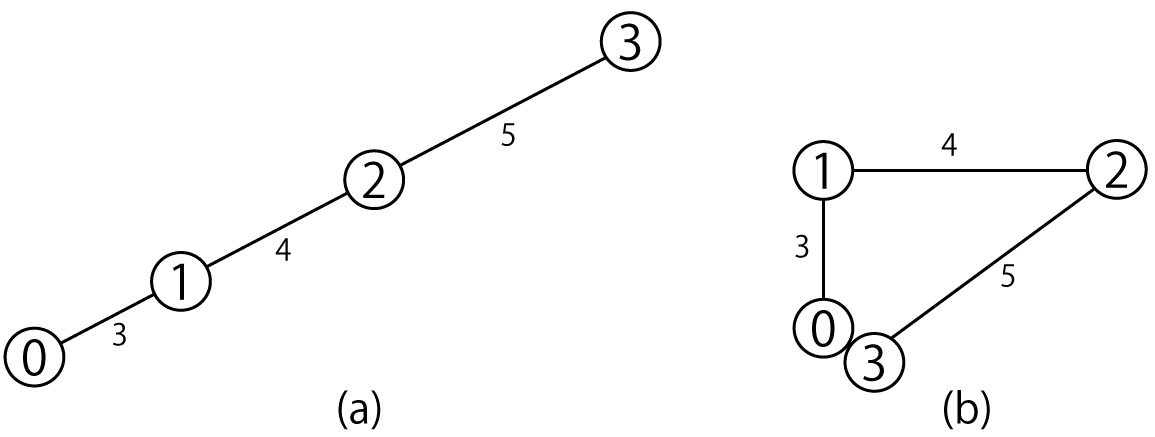
- 0 番の点と 3 番の点の間の距離が最も大きくなるのは、下図(a)のように 0 番の点と 3 番の点を端にして 4 点が一直線に並ぶ場合で、その距離は 3+4+5=12 となります。
- 0 番の点と 3 番の点の間の距離が最も小さくなるのは、下図(b)のように 0 番の点と 3 番の点の位置が等しい場合で、その距離は 0 となります。

入力例 3
2 512 512
出力例 3
1024 0
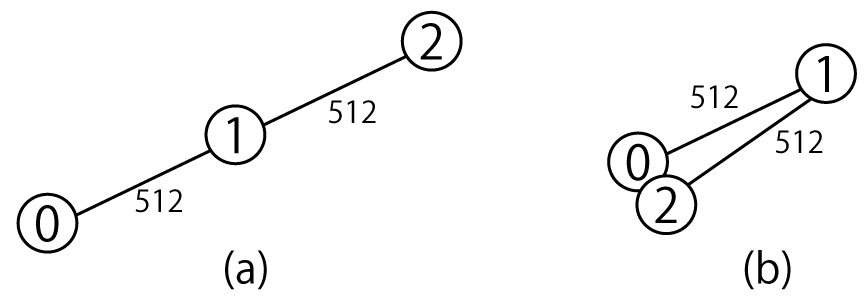
- 0 番の点と 2 番の点の間の距離が最も大きくなるのは、下図(a)のように 0 番の点と 2 番の点を端にして 3 点が一直線に並ぶ場合で、その距離は 512+512=1024 となります。
- 0 番の点と 2 番の点の間の距離が最も小さくなるのは、下図(b)のように 0 番の点と 2 番の点の位置が等しい場合で、その距離は 0 となります。

入力例 4
3 4 8 1
出力例 4
13 3
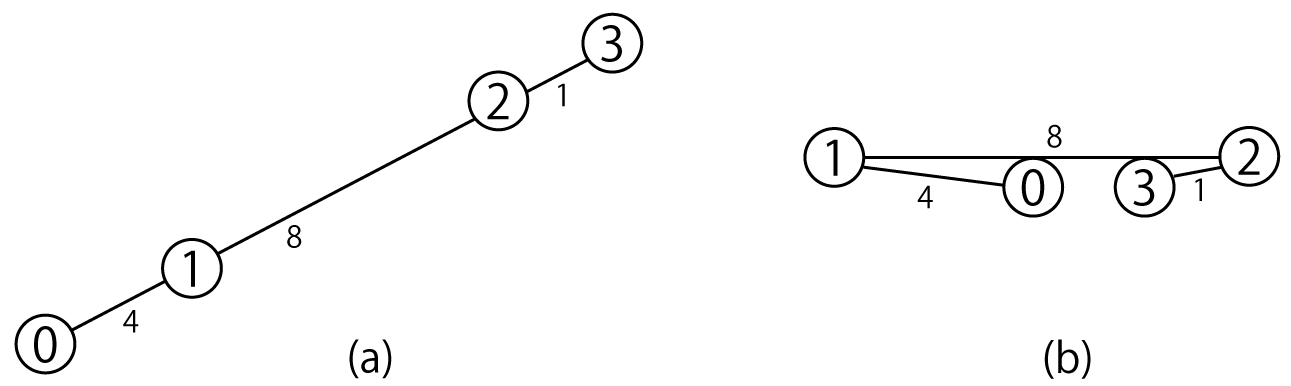
- 0 番の点と 3 番の点の間の距離が最も大きくなるのは、下図(a)のように 0 番の点と 3 番の点を端にして 4 点が一直線に並ぶ場合で、その距離は 4+8+1=13 となります。
- 0 番の点と 3 番の点は重なることができないので、0 番の点と 3 番の点の間の距離が最も小さくなるのは下図(b)のように 1 番の点と 2 番の点を繋ぐ線分上に 0 番の点と 3 番の点がある場合で、その距離は 8-4-1=3 となります。

入力例 5
10 1 2 3 4 5 6 7 8 9 10
出力例 5
55 0
- 0 番の点と 10 番の点の間の距離が最も大きくなるのは、0 番の点から 10 番の点が順に一直線に並ぶ場合で、その距離は 1+2+3+4+5+6+7+8+9+10=55 となります。
- 0 番の点と 10 番の点の間の距離が最も小さくなる一例は、0 番の点から 10 番の点まで順に円型に並び、0 番の点と 10 番の点の位置が等しくなった場合です。